THE BIRTH OF COMPUTING - TORRES QUEVEDO'S CALCULATING MACHINES
TORRES, M.L. (LEONARDO TORRES Y QUEVEDO).
Sur la constuction des machines algébriques. Extrait de la Revue de Mécanique, nos de septembre-octobre 1901.
Paris, 1901.
Small folio. Original printed wrappers. The fragile wrappers have been expertly restored along the edges. A stain to back wrapper, a closed horizontal tear, and spine re-enforced. A bit of soiling and discolouration. With a library-label to top of front wrapper, from the Bibliothèque des professeurs St-Stanislas, Mons, of which there is a book-plate to half-title and a stamp to title-page. Wrappers loose. Internally some brownspotting and finely restored marginal chipping, far from affecting text. 32 pp. Richly illustrated.
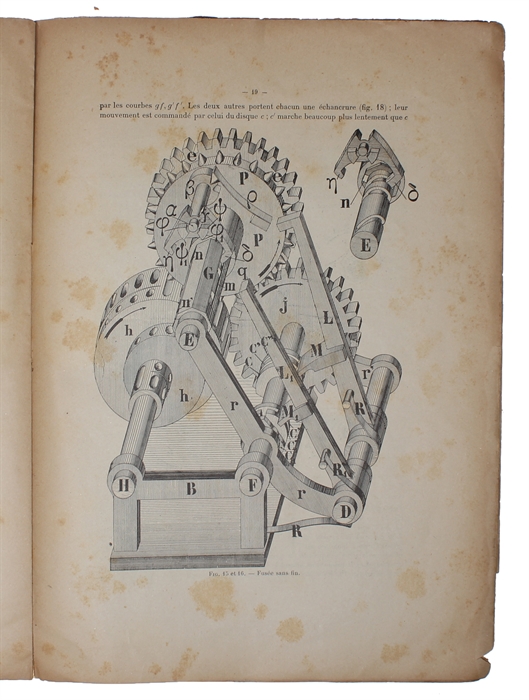
Exceedingly scarce original offprint of Torres y Quevedo's publication of his seminal algebraic machines, constituting a milestone in computing history. In this thoroughly illustrated publication, Torres y Quevedo explains the construction and operation of the first accurate calculating machines, following his explanation of them before the French Academy of Sciences earlier the same year. Leonardo Torres y Quevedo (1852 -1936), civil engineer and mathematician, was a one of the most important Spanish inventors of all time. Although little known outside of Spain and France in his life-time, he was an inventor of the utmost importance and would later be recognized as one of the most significant inventors of the beginning of the twentieth century. Apart from pioneering accurate automated calculation machines, he was also a pioneer in the development of the radio control, the inventor of a chess automaton (the first decision-making automaton), an innovative designer of the three-lobed non-rigid Astra-Torres airship as well as the Whirlpool Aero Car located in Niagara Falls, and with his Telekine, he created wireless remote-control operation principles. "Because of Torres Quevedo's work on analog machines, the Paris Academy of Sciences welcomed his "Calculating Machines" report in 1900. As a result, he was elected to the Academy of Sciences in Madrid in 1901, where he delivered a lecture on algebraic machines. The algebraic machine of Torres was an analog computing device, featuring a mechanism based on cone-shaped pulley with a helical groove around it. The machine was used for the resolution of equations like: + Ax = B or + Ax = B. His publications marked the beginning of a new era in mathematical theory, and his contributions resulted in the creation of cutting-edge new machinery. "Torres Quevedo's writings ushered in a new era in mathematical theory based on new concepts. His contributions led to the development of innovative new machines. "Leonardo Torres (1852-1936), usually known as Leonardo Torres y Quevedo in Spanish-speaking countries, was a Spanish engineer and mathematician. He was president of the Academy of Sciences of Madrid, a member of the French Academy of Sciences, and famous-mainly in Spain and France- as a prolific and successful inventor... Some of the earliest Torres' inventions took the form of mechanical analog devices, considered of great originality, aiming at implementing what he called the Algebraic Machine. This machine had the ability of computing the values of arbitrary polynomial functions in one variable. Since it was an analogue machine, the variable could attain any value, not only a preestablished set of discrete values, contrarily to what happened, for example, with the celebrated Babbage's Difference Engine, an engine that used the method of finite differences to generate successive values of polynomial functions. In Torres' Algebraic Machine, all quantities were represented by means of angular displacements in logarithmic scale. Then, adding a counter to keep track of the number of turns, it was possible to compactly represent very large variations for all quantities. When the wheel representing the variable spun round, the final result was obtained as the angular displacement of another wheel that accumulated the addition of all involved monomials. When this result was zero, a root of the function was found. Using proper modifications, it was even possible to obtain the complex roots. The use of logarithms had two main advantages. Firstly, assuming that all absolute errors for the angular displacements were constant, all relative errors for the represented quantities were also kept constant. Secondly, the computation of monomials was greatly simplified. Actually, the logarithm of a monomial of the form aixi is an expression, ai+ilogx, that can be easily calculated using a differential transmission. Nevertheless, the use of logarithms had a number of disadvantages. It was necessary to introduce some transformations to ensure that all quantities were positive and, what was much more challenging, it was necessary to design a sophisticated mechanical device able to compute log(a +b) from log(a) and log(b) that would permit to accumulate the sum of all involved monomials. This device was the endless spindle. In 1893, Leonardo Torres presented, before the Academy of Exact, Physical and Natural Sciences, a memoir on his Algebraic Machine. In his time, this was considered an extraordinary success for Spanish scientific production. In 1895 the machine was presented at a congress in Bordeaux. Later on, in 1900, he would present his calculating machine before the Paris Academy of Sciences." The present offprint, which richly illustrates, demonstrates, and presents his seminal calculating machines, was published after his presentation at the Academy of Sciences in Paris, and as he says in the preface to the present offprint "the theoretical principles of these machines have very recently been exposed in a mémoire entitled "Machines à calculer" [See Tomash & Williams: T 47, printed 1902], presented by me at the l'Académie des Sciences, which should appear also in the "Recueil des Savants étrangers." (own translation from p. (5) ). This publication is of the utmost scarcity, and we can locate merely two copies of this offprint: at the Torres y Quevedo-museum in Spain, and at the Hungarian Academy of Sciences.
"At the end of the nineteenth century, several analog machines had been proposed for solving algebraic equations. These machines -based not only on kinematics principles but also on dynamic or hydrostatic balances, electric or electromagnetic devices, etc.- had one important drawback: lack of accuracy. Leonardo Torres was the first to beat the challenge of designing and implementing a machine able to compute the roots of algebraic equations that, in the case of polynomials of degree eight, attained a precision down to 1/1000. The key element of Torres' machine was the endless spindle, an analog mechanical device designed to compute log(a +b) from log(a) and log(b). This short account gives a detailed description of this mechanism." (Federico Thomas: A Short Account on Leonardo Torres' Endless Spindle).
"Leonardo Torres was probably the most eminent Spanish engineer in the first half of the 20th century. He had a great influence, truncated by the Spanish Civil War, in the development of automatic control in Spain. As Randell points out in, we can only speculate on what might happened if Torres' writings had become better known to the English-speaking world. For instance, he qualifies Torres' paper Essays on Automatics as "a fascinating work which well repays reading even today." The paper contains what Randell believes to be the first proposal of the idea of floating-point arithmetic. It seems clear that Torres' contributions deserve much wider appreciation outside Spain". (Federico Thomas: A Short Account on Leonardo Torres' Endless Spindle).
The endless spindle was a critical component of the 8-term equation-solving computing machine. It created sums to answer the algorithm's central equation. The mechanism was the first of its sort, and it was the most intriguing and unique of Torres Quevedo's inventions.
Torres Quevedo's calculating machine was both theoretically and practically groundbreaking. The endless spindle is a mechanical device that evaluates an expression's logarithm as the sum of numerous logarithms, overcoming the difficulty of reaching enough precision with an automatic set of parts." (The History of the Computer)
He built a series of analog calculating machines to complement his theoretical work, all of which were mechanical." (Torres Quevedo Museum - where another copy of the present offprint is displayed)
Order-nr.: 60101