FORESHADOWING NON-EUCLIDEAN GEOMETRY

LAMBERT, JOHANN HEINRICH [NON-EUCLIDEAN GEOMETRY].

Observations Trigonometriques.

(Berlin, Haude & Spener, 1770). 4to. No wrappers, as issued in "Mémoires de l'Academie Royale des Sciences et Belles Lettres", tome XXIV, pp. 327-354 and 1 engraved plates.

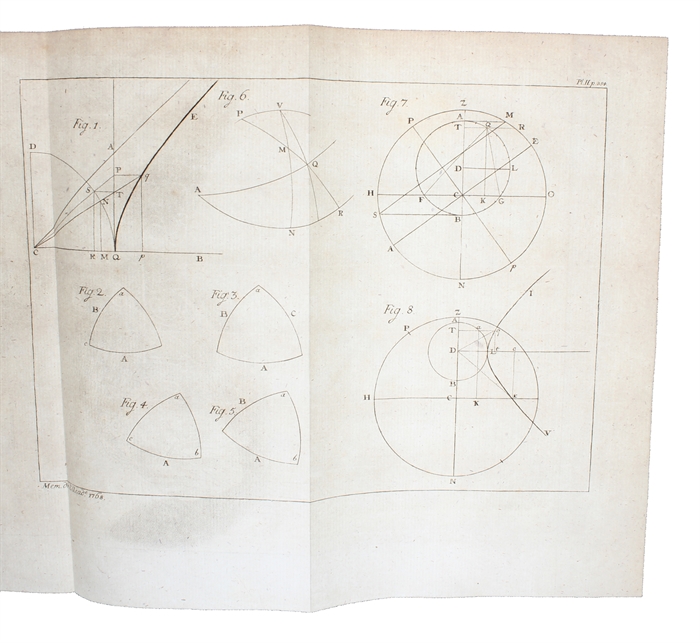
First edition. Lambert's work on non-Euclidean geometry is among the most important in the field. Carl Boyer writes "No one else came so close to the truth without actually discovering non-Euclidean geomtry." (History of Mathematics, pp. 504). Lambert wrote his famous book 'Theorie der Parallellinien' in 1766, but it was not published until 1786 (nearly a decade after his death). Lambert originally set out to prove Euclid's parallel postulate in a similar way to that which Saccheri had used in his 'Euclides Vindicatus', but in contrast he did not interpret the consequences of non-Euclidean geometry as absurd. The offered paper ('Observations Trigonometriques') is the only work by Lambert on non-Euclidean geometry which was published during his life-time. Here he made the important discovery of the duality between spherical and hyperbolic geometry, i.e., that hyperbolic trigonometries can be deduced from spherical trigonometries by using imaginary angles (and consequently he introduced the hyperbolic functions, for the first time). By illustrating this duality Lambert gave strong evidence of the consistency of non-Euclidean geometries. (See Kline's Mathematical Thought from Ancient to Modern Times, pp. 404 & 868).

Order-nr.: 31785